在电磁学的广阔天地中,磁感应强度是一个核心概念,它描述了磁场对运动电荷的作用力。而磁感应强度的散度等于零这一特性,是磁场理论中的一个基本原理,它揭示了磁场线无源性的本质。本文将围绕这一主题,结合《张朝阳的物理课》中对毕奥萨伐尔定律的介绍,深入探讨磁感应强度散度为零的原因及其物理意义。
1. 磁感应强度与散度
我们需要明确磁感应强度(
B
)的定义。在物理学中,磁感应强度是一个矢量场,它描述了空间中每一点磁场的强度和方向。磁感应强度的散度(divB
)是一个标量,它衡量了磁场在空间中每一点的变化率。2. 毕奥萨伐尔定律
毕奥萨伐尔定律是电磁学中的一个基本定律,它描述了电流元在空间中产生的磁场。根据这一定律,一个电流元
Idl
在距离r
处产生的磁感应强度dB
可以表示为:\[ dB = \frac{\mu_0}{4\pi} \frac{Idl \times \hat{r}}{r^2} \]
其中,\(\mu_0\)是真空磁导率,
Idl
是电流元,\(\hat{r}\)是单位向量,指向观察点。3. 磁感应强度散度为零的证明
要证明磁感应强度的散度等于零,我们可以从毕奥萨伐尔定律出发。考虑一个闭合回路中的电流分布,根据毕奥萨伐尔定律,整个回路产生的磁场可以通过积分得到。由于磁场是由电流产生的,而电流是闭合的,因此磁场线也是闭合的。
在数学上,散度定理(高斯定理)表明,矢量场的散度可以通过对该场在闭合曲面上的通量进行积分得到。由于磁场线是闭合的,它们在任何闭合曲面上既不会产生也不会消失,因此磁感应强度的散度在任何点都为零。
4. 物理意义
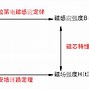
磁感应强度的散度等于零这一特性,反映了磁场的无源性。在自然界中,电荷可以单独存在,从而产生电场,电场的散度不为零。然而,磁单极子(即单独的北磁极或南磁极)至今未被发现,所有的磁场都是由电流产生的,而电流总是成对出现,形成闭合回路。因此,磁场线总是闭合的,没有起点也没有终点,这就是磁感应强度散度为零的物理根源。
5. 结论
通过《张朝阳的物理课》中对毕奥萨伐尔定律的介绍,我们不仅理解了磁感应强度散度为零的数学证明,更重要的是,我们洞察了这一现象背后的物理本质。磁场的无源性是电磁学中的一个基本原理,它不仅在理论上有着深远的影响,也在实际应用中,如电机、变压器和磁共振成像等领域,发挥着至关重要的作用。
通过深入探讨磁感应强度散度为零的原因,我们不仅加深了对电磁学基本定律的理解,也为进一步探索电磁现象提供了坚实的理论基础。











