小米确定造车或由雷军带队

从麦克斯韦方程组推导出光波方程

引言：

麦克斯韦方程组是描述电磁场的基本方程组，它由四个方程组成。而光波方程描述了电磁波在介质中的传播行为。本文将通过推导的方法展示如何从麦克斯韦方程组中得到光波方程。

1. 麦克斯韦方程组回顾：

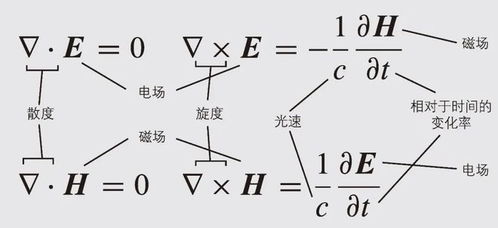
麦克斯韦方程组由以下四个方程组成：

a) 高斯定理：$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$

b) 安培定理：$\nabla \cdot \mathbf{B} = 0$

c) 法拉第电磁感应定律：$\nabla \times \mathbf{E} = \frac{\partial \mathbf{B}}{\partial t}$

d) 法拉第电磁感应定律（微分形式）：$\nabla \times \mathbf{B} = \mu_0 \mathbf{J} \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}$

其中，$\mathbf{E}$ 是电场强度，$\mathbf{B}$ 是磁感应强度，$\rho$ 是电荷密度，$\mathbf{J}$ 是电流密度，$\varepsilon_0$ 是真空介电常数，$\mu_0$ 是真空磁导率。

2. 推导步骤：

为了得到光波方程，我们首先将上述方程组中的电场强度 $\mathbf{E}$ 和磁感应强度 $\mathbf{B}$ 表示为复数形式，即 $\mathbf{E} = \mathbf{E}_0 e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$ 和 $\mathbf{B} = \mathbf{B}_0 e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$，其中 $\mathbf{E}_0$ 和 $\mathbf{B}_0$ 是复振幅，$\omega$ 是角频率，$\mathbf{k}$ 是波矢量，$\mathbf{r}$ 是位置矢量。

3. 高斯定理的推导：

将复数形式的电场强度 $\mathbf{E}$ 代入高斯定理中的左侧，得到：

$\nabla \cdot \mathbf{E} = \nabla \cdot (\mathbf{E}_0 e^{i(\omega t \mathbf{k} \cdot \mathbf{r})})$

利用矢量公式 $\nabla \cdot (\mathbf{A} e^{i\mathbf{k} \cdot \mathbf{r}}) = (\mathbf{k} \cdot \mathbf{A}) e^{i\mathbf{k} \cdot \mathbf{r}}$，其中 $\mathbf{A}$ 是任意矢量，可以得到：

$\nabla \cdot \mathbf{E} = (\mathbf{k} \cdot \mathbf{E}_0) e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$

将高斯定理中的右侧 $\frac{\rho}{\varepsilon_0}$ 表示为复数形式 $\frac{\rho_0}{\varepsilon_0} e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$，其中 $\rho_0$ 是电荷密度的复数振幅，可以得到：

$(\mathbf{k} \cdot \mathbf{E}_0) e^{i(\omega t \mathbf{k} \cdot \mathbf{r})} = \frac{\rho_0}{\varepsilon_0} e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$

通过对比两边的指数因子，我们可以得到关系式 $(\mathbf{k} \cdot \mathbf{E}_0) = \frac{\rho_0}{\varepsilon_0}$。这是高斯定理在复数形式下的形式。

4. 安培定理的推导：

在复数形式下，$\nabla \cdot \mathbf{B} = 0$ 仍然成立。

5. 法拉第电磁感应定律的推导：

将复数形式的电场强度 $\mathbf{E}$ 和磁感应强度 $\mathbf{B}$ 分别代入法拉第电磁感应定律的左侧和右侧，得到：

$\nabla \times \mathbf{E} = i\omega\mathbf{B}_0 e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$

$\nabla \times \mathbf{B} = i\omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0) e^{i(\omega t \mathbf{k} \cdot \mathbf{r})}$

将左右两侧的指数因子进行对比，我们可以得到关系式 $\mathbf{k} \times \mathbf{E}_0 = \omega\mathbf{B}_0$ 和 $\mathbf{k} \times \mathbf{B}_0 = \omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0)$。

6. 光波方程的推导：

将关系式 $\mathbf{k} \times \mathbf{E}_0 = \omega\mathbf{B}_0$ 和 $\mathbf{k} \times \mathbf{B}_0 = \omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0)$ 代入到法拉第电磁感应定律的右侧，我们可以得到：

$\nabla \times (\nabla \times \mathbf{E}) = i\omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0)$

应用矢量公式 $\nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) \nabla^2 \mathbf{A}$，其中 $\mathbf{A}$ 是任意矢量，我们可以将上述方程进一步简化为：

$\nabla (\nabla \cdot \mathbf{E}) \nabla^2 \mathbf{E} = i\omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0)$

根据高斯定理 $\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$，我们可以将上式进一步简化为：

$\nabla^2 \mathbf{E} = i\omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0)$

在真空中 $\mathbf{J}_0 = \mathbf{0}$，并且考虑到光速 $c = \frac{1}{\sqrt{\varepsilon_0\mu_0}}$，我们可以得到光波方程：

$\nabla^2 \mathbf{E} \frac{1}{c^2}\frac{\partial^2 \mathbf{E}}{\partial t^2} = \mathbf{0}$

类似地，通过将关系式 $\mathbf{k} \times \mathbf{E}_0 = \omega\mathbf{B}_0$ 和 $\mathbf{k} \times \mathbf{B}_0 = \omega\mu_0 (\mathbf{J}_0 \varepsilon_0 \mathbf{E}_0)$ 代入到法拉第电磁感应定律（微分形式）的右侧，并简化计算，可以得到光波方程：

$\nabla^2 \mathbf{B} \frac{1}{c^2}\frac{\partial^2 \mathbf{B}}{\partial t^2} = \mathbf{0}$

结论：

从麦克斯韦方程组中，我们推导出了光波方程。光波方程描述了电磁波在介质中的传播行为，它对于理解光的传播和各种光学现象非常重要。在实际应用中，我们可以通过解光波方程来研究电磁波在不同介质中的传播特性，并应用于光通信、光传感等领域的设计和优化。

《张朝阳的物理课》介绍麦克斯韦方程组